More is different.

作者简介 

本文作者梅拉妮·米歇尔为波特兰州立大学计算机科学教授，圣塔菲研究所客座教授，曾就读于「集异壁」作者侯世达门下。

图书简介

本书深入浅出的介绍了复杂学科的历史背景、研究内容和挑战，是一本相当优秀的科普读物。从复杂学科产生原因讲起，依次介绍了复杂学科的一些较为成功的模型，比如元胞自动机，小世界网络，无尺度网络，随机布尔网络等。

导读

刚下过一场小雨，天空正在变晴，空气还是湿漉漉的，落叶上的水珠苍翠欲滴。这是难得的空闲，你点上一支烟，抬起了头。今天的天空有些奇怪，那蓝色似乎与往日不同。失真的色彩让你陷入了沉思，往事如潮水般纷至沓来。

沉寂中，旁边的同伴碰了你一下，思绪戛然而止。这是寻找食物的信号，是时候开始工作了，你用中脚踩灭了烟头。

「我的人生毫无意义，简直就像蚂蚁一样。」你郁闷的嘟囔着。

哦不对，我就是只蚂蚁，一只节肢动物门昆虫纲膜翅目行军蚁。

行军蚁是世界上已知行动最简单的动物，如果将 100 只行军蚁放在一个平面上，它们会不断往外绕圈，直至力竭而死。然而，如果将上百万只放到一起，群体就会组成一个整体而形成具有「集体智慧」的「超级生物」。有趣的是，这种由大量个体形成网络，不存在中央控制，通过简单运作规则产生出复杂集体行为和复杂信息处理的系统在自然界处处可见。数以亿计的神经元通过相互之间简单的信息传递，形成了精致的大脑；免疫细胞通过互相传递化学物质，为生命体安全提供高效的保障；昆虫群落经由个体之间的简单通信，作为一个整体在自然界险中求生。本书所要阐述的，就是这种涌现宏观行为和自组织行为的复杂系统产生的原因。

解析梦的破碎

既然个体的行为如此简单，如果我们能够知道所有的初始条件，那么岂不是就可以求得所有的结果了？玻尔兹曼之前的物理学就是这样的思路。1665 年，年轻的牛顿在乡下躲避瘟疫时，创立了万有引力定律，接过了开普勒天空立法者的王冠，开始支配宇宙万物的运动，那是物理学家最意气风发的时代，他们鲜衣怒马，挥斥方遒，万物在他们的笔下褪去神秘的面纱。1814 年，被誉为法国牛顿的拉普拉斯则更进一步，断言如果我们能够知晓宇宙所有粒子的当前位置和速度，原则上就有可能预测任何时刻的情况。

当然事实上我们并不能做到，量子力学的发展否定了拉普拉斯的假设，我们无法同时准确的知道一个粒子的当前位置和速度。后来统计物理另辟新径，不关心各个分子具体的位置、速度和未来的变化，而去预测大量分子整体上的平均位置和速度，从而较好的解释了很多热学现象。

如果说统计物理研究的是大量随机运动的物理整体上表现出来的物理现象，那么如果是确定性的运动，是否我们就能得到解析解呢？拉普拉斯如此笃定，这一梦想却很快被庞加莱击碎。牛顿力学几乎是完美的解决了两个物体的运动问题，但没想到三体要复杂的多。庞加莱在尝试解决这个问题时，发现了对初始条件的敏感依赖性。本书以人口模型为例说明了确定条件导致混沌的这一现象。马尔萨斯的人口模型认为人口的增长率是固定不变的值，即次年人口＝当年人口 $\times$ 增长倍率。那么，人口便呈几何速率增长。这一模型可以很好的解释 1860 年之前的人口发展现象，但之后的偏差越来越大。Logistic 模型是对这一模型的改进。该模型加入阻滞增长因子，即人口的增长会阻滞其增长速率，且环境有最大容许的人口限度，超过最大限度，整个族群将走向灭亡。然而，对这一模型的研究发现，当初始增长率满足一定条件时，人口增长的曲线将会随着人口初始值的微小变动呈现出极大的震荡。也就是说，我们没有办法通过观察某些年的人口数变化来推测出这个初始值和初始增长率—这就是确定性导致的混沌现象。

和意气风发的拉普拉斯一样，1900 年的希尔伯特雄心勃勃。在拉普拉斯眼里，物理法则是完备的，只要条件充足，我们就可以知道过去和未来的一切。希尔伯特对此表示赞同。他还认为，数学是一致和完备的，全部数学的相容性都可以归结为基本算术的相容性。罗素也认为，可以建立逻辑主义数学体系，从而将整个数学归纳为逻辑学。这一年，希尔伯特在巴黎的数学家大会上提出了 23 道最重要的数学问题，其中部分可以总结为三个问题：数学是不是完备的；数学是不是一致的；是不是所有命题都是数学可判定的。这三个问题过了 30 年也没有能够解决，但是希尔伯特很有信心，认为答案一定是「是」。不幸的，或者说幸运的，这个梦想并没有实现。1931 年，25 岁的哥德尔漂亮地证明了两条不完备定理，破坏了希尔伯特计划的哲学企图。哥德尔的证明意义非常深远，以至于几十年后，在一个蝉声聒噪的午后，「GEB」的作者侯世达在一家书店偶然看到了「哥德尔的证明」一书，被他的理论震动，从而对相关命题产生了浓厚的兴趣。让我们记住这个平凡的下午，它将在未来关键的历史时刻多次重现。

除了不完备，不确定和混沌，令人受挫的还有复杂的难以度量的特性。虽然科学家提出了按照熵、算法信息量、逻辑深度、分形维度等来尝试度量复杂，但是似乎每种度量方法都有致命的缺陷。复杂嵌套复杂，唯一看起来不那么复杂的，就是复杂所涌现的宏观表象，似乎很有规律可循。

模型的建立

下起了雨/慌乱中爬过的蚂蚁/它的鼻子在寻找谁的气息

— 李志「下雨」

可计算性是一门学科能否快速发展的关键要素之一，生物技术正是得益于基因的发现从而快速发展。复杂科学的可计算性又在哪里呢？对复杂的度量困难重重，我们不妨再次回到蚂蚁身上来。2002 年「科学」杂志发表了一篇题为「社会性昆虫行为的计算」的文章，文中昆虫学家将蚂蚁群体的行为等同于「计算机算法」，每只蚂蚁都执行简单的程序，没有中央控制，使得整个种群作为一个整体执行复杂的计算。类似的，1994 年 3 位大脑科学家也提出，大脑的计算方式—亿万神经元并行工作，无须中央控制—和蚁群的运作十分相像。而描述这一现象的一种较好的数学模型就是元胞自动机。

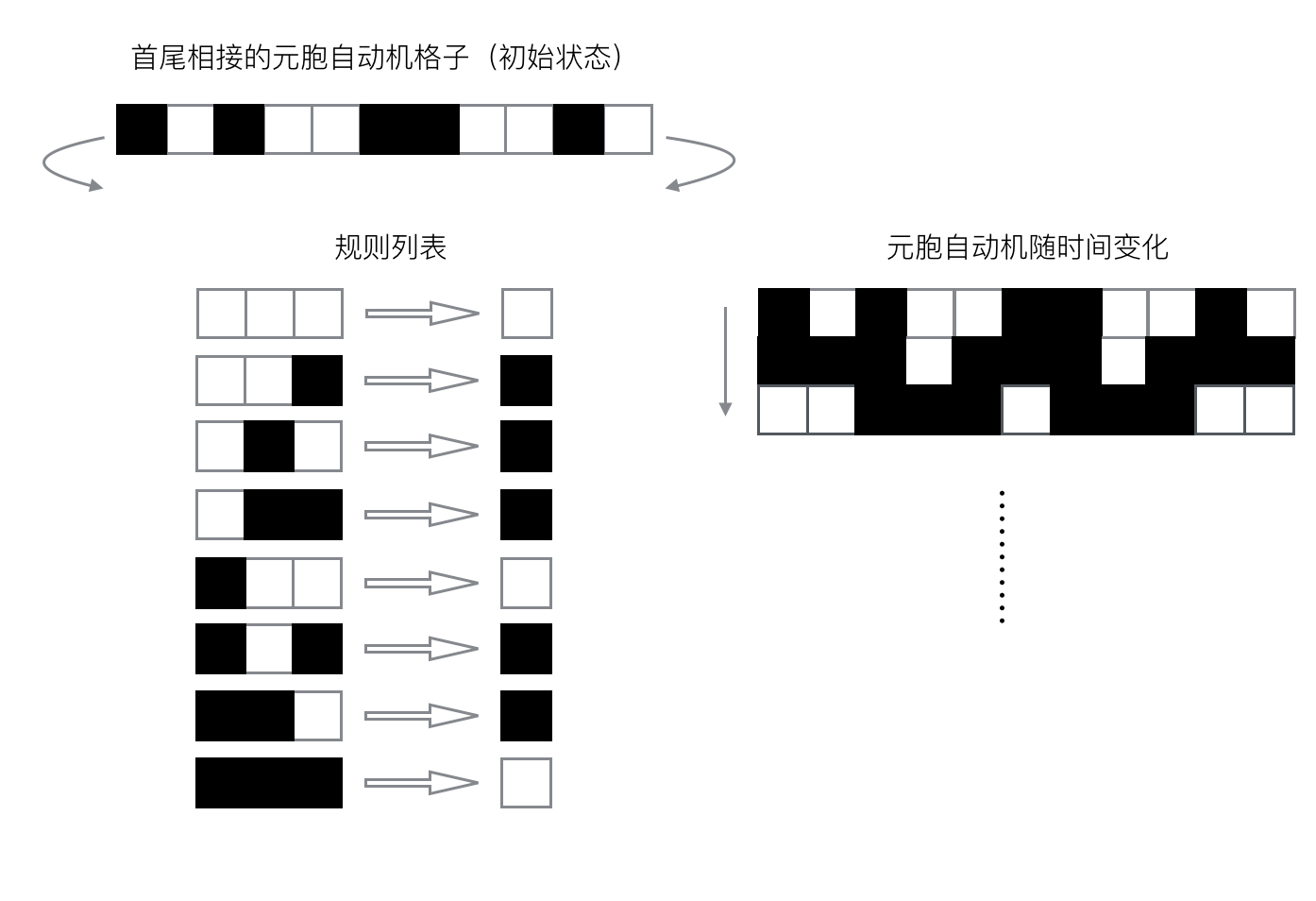
元胞自动机描述了一个元胞矩阵，在这个矩阵中，每个元胞的下一步的状态，都由自己和周围的 8 个元胞的当前状态所决定。每一种组合态和其对应的下一步状态都是一种规则，显而易见，这种规则的数量极为庞大。

元胞自动机是复杂系统的理想模型¹。同自然界的复杂系统一样，元胞自动机也是由大量简单个体组成，不存在中央控制，每个个体都只与少量其他个体交互，而且元胞自动机也能表现出非常复杂的行为，它们的行为甚至不可能通过更新规则预测。

一些爱好者简化了元胞自动机的规则，发展了很多有趣的实验和游戏(康威生命游戏)。但却一直没能找到合理解释元胞自动机工作原理的理论。克鲁奇菲尔德提出可以按照研究动力系统行为的「信息处理结构」来分析遗传算法演化出的元胞自动机。在这种思想下，元胞自动机状态的改变在宏观上的表现被具象化为粒子的碰撞、湮灭和延续²，在一定程度上可以解释元胞自动机的原理³。

在这里，生物系统的遗传和变异也找到了意义。元胞自动机的规则数量如此庞大，对于设定的目标，必然大部分规则都无法实现，甚至部分规则都无法收敛于一个稳定的状态。而对生物系统而言，借由自然选择和基因遗传，只有符合当前目标的高效的规则簇才可能存活。但随着时代的发展，最核心的目标也在变化，如果没有变异，那么千年万年前形成的规则将不再适应当前的核心目标。寻找更加高效的规则，并遗传下去，同时不放弃其他暂时不高效的规则，这就是遗传算法演化的元胞自动机状态，也是生命得以延续的方式。

没有中央控制，个体都只与少量其他个体交互的元胞自动机模型可以很好的描述很多生物学现象。通过免疫系统、蚁群工作和新陈代谢三个例子，作者试图说明「信息」在系统中扮演的角色，信息传递和处理的方式以及信息的意义。在这样的系统中，信息不再像传统计算机系统那样位于某个具体的位置，而是表现为系统组分的动态模式和统计结果。1. 系统中，信息通过个体对时间和空间的采样来传递；2. 个体的采样（探测）行为具有随机性；3. 复杂系统绝大多数具有微粒化结构，个体以高度并行的方式协同工作；4. 根据系统的需要，分散探测与集中行动之间不断进行互动。

人工智能的先驱之一明斯基曾简明扼要地总结 AI 的悖论为：「容易的事情很难」。即计算机可以很轻易的做很多对人类来说十分复杂和棘手的工作，但是却无力处理一些连三岁小孩都能做的事情。作者受上述例子启发，在导师侯世达的指导下，利用复杂模型的四个特点：随机探测，实时协作，时空采样和切换分散与集中行动，设计了一套算法实现了对人类来说很正常的类比功能。人类的类比能力是否基于这一算法，我们并不清楚，但这无疑是模拟人类能力的重要尝试。

雨后湿润的空气凉爽清新。放大镜下的蚂蚁似乎停止了休息，开始忙碌起来。你收起放大镜，深深的嗅了嗅泥土的芳香，对同伴说：「这些蚂蚁生活没有目的，没有爱，有些甚至没有性别，它们能感受到幸福吗？」同伴摇了摇头，「感受幸福需要意识的吧，蚂蚁没意识的。」「话说回来，什么叫意识呢？」

事实上，作者一直避免探讨信息的意义。比如，上述实现了类比功能的算法，我们认为计算机虽然可以得到较为满意的结果，但是它并不理解这个结果。而对于我们人类来说，当我们说「鞋子之于脚就像手套之于手」，我们认为自己确切的了解这句话的意思，而计算机不会。AI 的终极目标是让人摆脱意义的怪圈，并且让计算机理解意义，这是 AI 中最难的问题。作者认为，也许类比将是解决问题的关键。

网络

DNA 是自我储存和复制的代码，生命是诞生在信息洪流中的一个节点。–攻壳机动队

在元胞自动机中，每个个体是平等的，状态值由相邻个体决定。这一模型似乎过于简单，无法更准确的描述现实世界中的网络。哈佛大学心理学家米尔格兰姆设计了一个实验，发现在人际关系中，平均经过 5 个熟人，一个人就可以达到另一个陌生人：我们似乎生活在一个小世界中。这个发现后来被称为六度分隔。

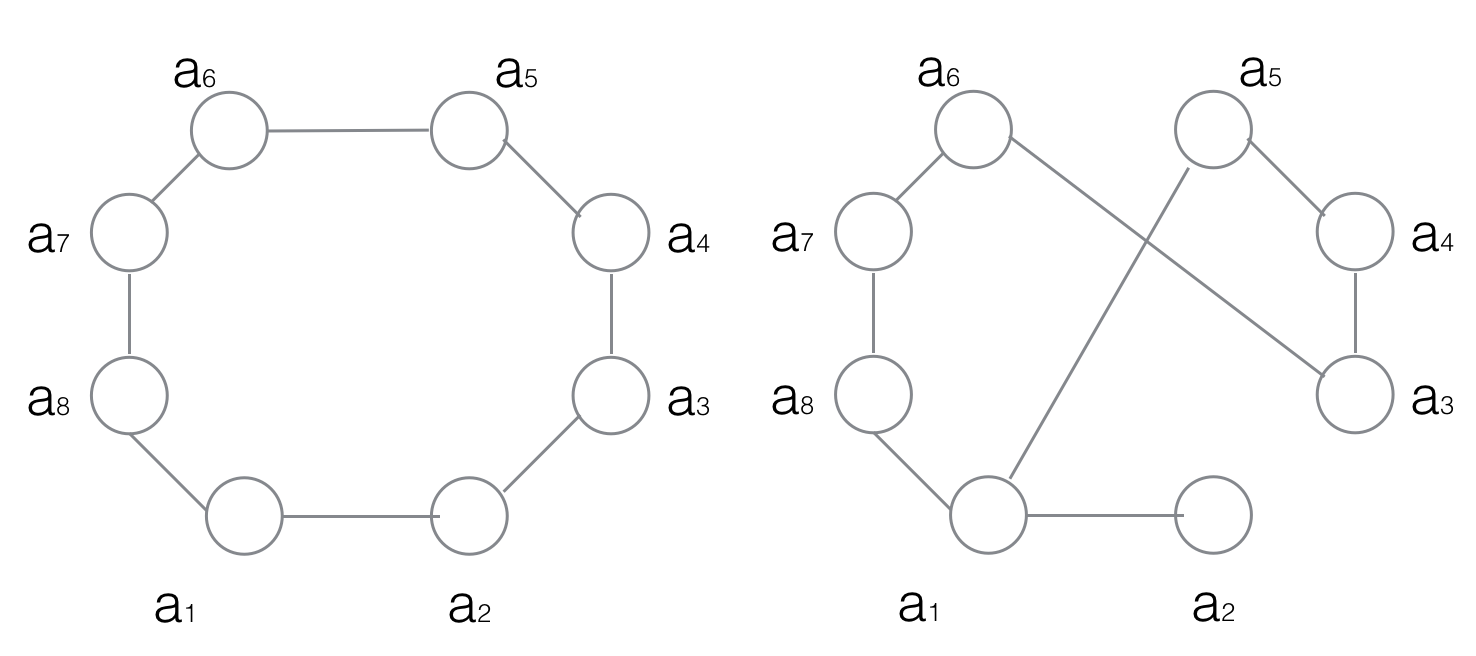
虽然后来的学者针对这个实验提出了诸多质疑，六度分隔也被认为并不可信，但是小世界的概念已深入人心。这些网络问题吸引了大批复杂系统研究者，关于网络科学的各种发现迅速涌现。邓肯·瓦特和斯托加茨率先从数学上定义了小世界网络的概念。在元胞自动机模型中，每个节点只和附近的一些节点有关。但在小世界网络模型中，我们选取部分连接，打断并重新连接。重连后的网络与原来的规则网络的连接数一样多，但是两个节点的平均路径长度大大下降。即小世界网络拥有这样的特性：网络只有少量的长程连接，相对于节点数量来说平均路径却很短。如下图所示，每条边的长度都相同，左边是邻点相接的普通网络，右边是部分边打断重连的小世界网络，右边网络的两点之间平均距离要小于左边的网络。而且，节点数越多，这种效果越明显⁴。（后续研究表明这种随机重连的方法有局限性⁵）

也许是某个蝉声悠悠的午后，「复杂：诞生于秩序与混沌边缘的科学」一书（复杂科学书籍的源头）的作者在演讲后安静地等待观众的提问。年轻的梅拉妮·米歇尔，也就是本书的作者，问到：「作为个体，是否有程度上的差异？」

时光荏苒，当初提问的年轻女士，如今已是该领域的权威了。

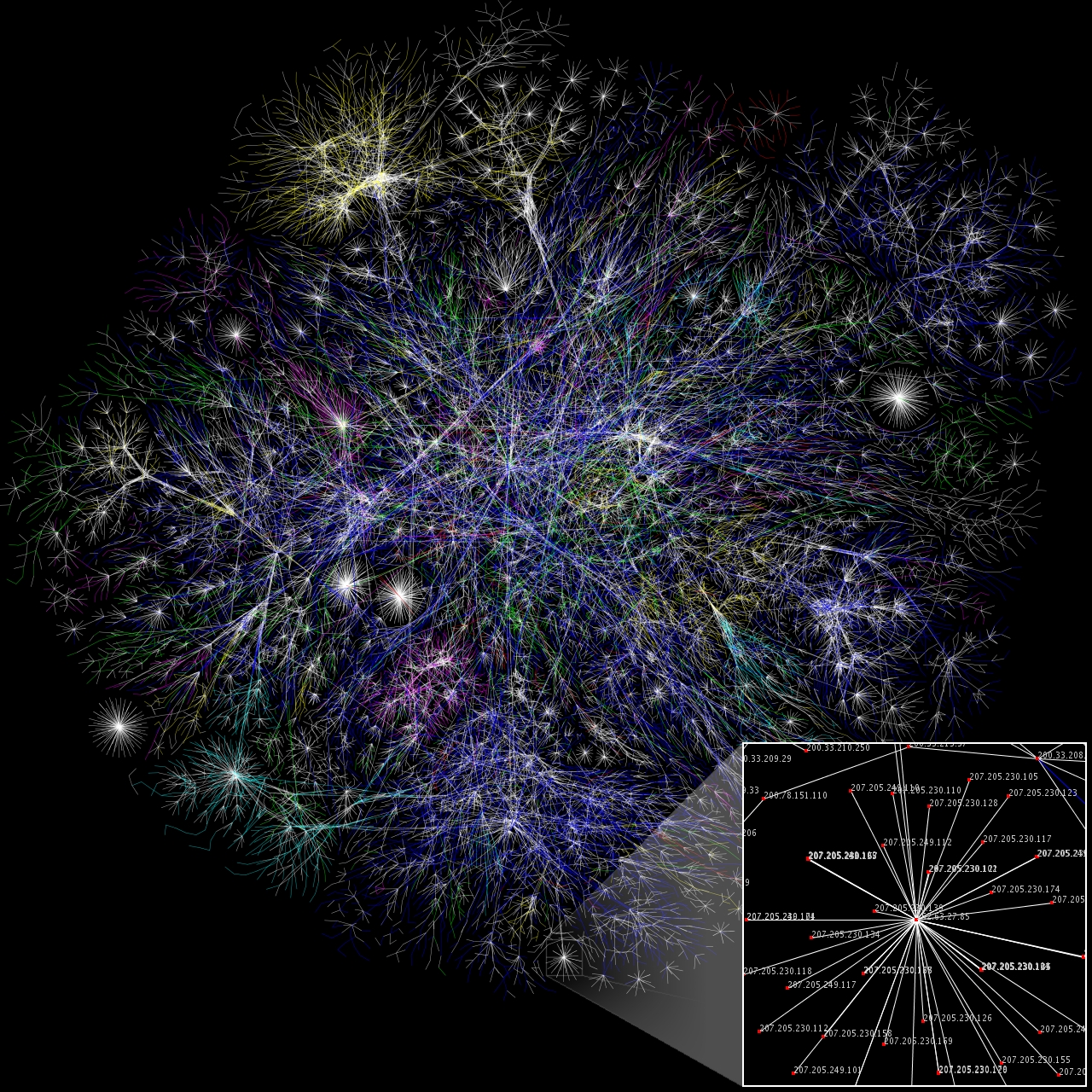
两位学者的论文引发了网络科学研究的热潮，科学家们在现实世界中发现了越来越多的小世界网络，比如美国西部电网，电影明星表演圈等等。然而进一步的研究表明，根据瓦特和斯托加茨提出的规则所生成的网络与许多真实世界网络的度分布并不一样。易知，小世界模型的节点的度分布较为平均，而很多真实网络并非如此：显然，作为个体，是有程度上的差异的。以我们熟悉的万维网为例，像谷歌这样的网站，它的入度必然远远超过大部分普通网站。一些团体的研究表明，入度为 $k​$ 的网页数量正比于 $k^{-2}​$。当我们在这个函数中截取不同的尺度时，我们惊奇的发现，截取到的图形几乎一模一样，在不同尺度下，图形具有自相似性（如下图所示）。也就是说，从表现上来看，这样的网络是无尺度的，这样的网络也自然的被称为无尺度网络。在数学上，无尺度网络就是连接度为幂律分布的网络，即入度为 $k​$ 的节点数量正比于 $k^{d}​$。指数 $d​$ 就是这种分布的关键。

拥有小世界和无尺度特性的网络具有稳健性，连接度无尺度分布、集群性和存在中心节点是共同的主题。按照幂律，重要的节点（入度很大）往往很少，大量的节点入度很小，这保证了网络不会轻易的崩溃。网络思想为许多困难问题提供了新的思路，比如更高效的搜索，控制流行病，管理大型组织等等。

网络科学为生物的比例之谜提出了一种新颖的解释。所谓比例之谜，指的是，动物的代谢率随着体型增大，也会相应的增加。但是，数据显示，动物的代谢率既不是正比于体积（考虑到动物密度相差不大，可以认为正比于体重），也不是正比于表面积（正比于体重的 $2/3$ 次幂），动物的代谢率正比于体重的 $3/4$ 次幂。更多的研究发现，$3/4$ 幂律不仅哺乳动物和鸟类成立，对鱼类、植物，甚至单细胞生物也成立。除此之外，动物的生命周期，心率等数据也和体重呈幂律关系，而且都是分母为四的分数形式。四分幂律是生物非常重要的共性，但是没人知道是什么共性。

新墨西哥大学的生态学教授布朗和其研究生恩奎斯特认为，向细胞输送营养的系统结构是解决问题的关键。在理论物理学家韦斯特的帮助下，提出了代谢比例理论。代谢比例理论假设：1.循环和营养输送系统能尽可能地填充身体空间；2.进化出的网络能最小化向细胞输送养分时所花费的能量和时间；3.网络向身体组织提供燃料的「终端单元」大小不随体重变化。

分形分支结构就是一种能尽可能填充空间的几何对象。三人小组最终的计算表明，决定代谢率的养分输送速率与体重呈指数为 $3/4$ 的比例关系。这意味着，虽然生物是三维的，其内部的生理结构和运作却表现为四维。体重是一个生命体的四维变量，营养输送速率和生命体的「表面积」：也就是体重的 $3/4$ 次幂成正比例。

继布朗、恩奎斯特和韦斯特提出代谢比例理论以来，越来越多的科学家开始使用该理论解释一些动物学上的比例现象，比如心率、生命期、妊娠期以及睡眠时间等。甚至植物学里的植物生长速度、树干周长，微观领域里的单细胞生物代谢率、DNA 变化速率等等也开始使用该理论解释。一个理论声称能够解释这么多现象，难免遭到大量的质疑。但它凭借独特的视角和较好的数据吻合度也征服了大批科学家，关于代谢理论的争论仍未结束。

大统一理论，为了人类心智的荣耀

复杂科学发展迅速，但却饱受争议。我们还不知道如何度量复杂，甚至连复杂科学的基本要素是什么都不清楚，更遑论给复杂科学找到一个统一理论了。复杂科可能在等待一位天才的降临。他或许是卡诺，提出了热力学的关键概念，使得热力学成为现代科学；或许是牛顿，不仅创造了词汇，还发展了微积分这门语言，建造出宏伟的动力学体系。

在这里我想用钱德拉塞卡的「莎士比亚、牛顿和贝多芬」一书中的一段结尾：

有谁不知道麦克斯韦关于气体动力学理论的论文呢？……速度的变量在一开始就被庄严宏伟地展现出来，然后从一边切入了状态方程，从另一边又切入了有心场的运动方程。公式的混乱程度有增不已。突然，定音鼓敲出了四个音节：令「$n=5$」。不祥的精灵 $u$（两个分子的相对速度）隐去了；同时，就如像音乐中的情形一样，一直很突出的低音突然沉寂了，原先似乎不可被超越的东西，如今被魔杖一挥而被排除。一个个的结论接踵而至，最后，意外的高潮突然降临，热平衡条件和输运系数的表达式出现，接着，大幕降落！

复杂科学的 $n=5$，不妨由你来给出。